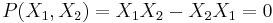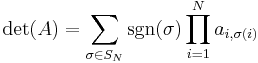Polynomial identity ring
In mathematics, in the subfield of ring theory, a ring R is a polynomial identity ring if there is, for some N > 0, an element P other than 0 of the free algebra, Z<X1, X2, ..., XN>, over the ring of integers in N variables X1, X2, ..., XN such that for all N-tuples r1, r2, ..., rN taken from R it happens that
Strictly the Xi here are "non-commuting indeterminates", and so "polynomial identity" is a slight abuse of language, since "polynomial" here stands for what is usually called a "non-commutative polynomial". The abbreviation PI-ring is common. More generally, the free algebra over any ring S may be used, and gives the concept of PI-algebra.
If the degree of the polynomial P is defined in the usual way, the polynomial P is called monic if at least one of its terms of highest degree has coefficient equal to 1. The PI-rings are usually taken as close generalizations of commutative rings. If the ring has characteristic p different from zero then it satisfies the polynomial pX = 0. To exclude these examples, sometimes it is defined that PI-rings must satisfy a monic polynomial identity.[1]
Contents |
Examples
- For example if R is a commutative ring it is a PI-ring: this is true with
- A major role is played in the theory by the standard identity sN, of length N, which generalises the example given for commutative rings (N = 2). It derives from the Leibniz formula for determinants
- by replacing each product in the summand by the product of the Xi in the order given by the permutation σ. In other words each of the N! orders is summed, and the coefficient is 1 or −1 according to the signature.
-
- Failed to parse (unknown function\dotsm): s_N(X_1,\ldots,X_N) = \sum_{\sigma \in S_N} \sgn(\sigma) X_{\sigma(1)}\dotsm X_{\sigma(N)}=0~
- The k×k matrix ring over any commutative ring satisfies a standard identity; the Amitsur–Levitzki theorem states that it satisfies s2k. The degree of this identity is optimal since the matrix ring can not satisfy any monic polynomial of degree less than 2k.
- Given a field k of characteristic zero, take R to be the exterior algebra over a countably infinite-dimensional vector space with basis e1, e2, e3, ... Then R is generated by the elements of this basis and
-
- eiej = −ejei.
- This ring does not satisfy sN for any N and therefore can not be embedded in any matrix ring. In fact sN(e1,e2,...,eN) = N!e1e2...eN ≠ 0. On the other hand it is a PI-ring since it satisfies [[x, y], z] := xyz − xzz − zxy + zyz = 0. It is enough to check this for monomials in the e's. Now, a monomial of even degree commutes with every element. Therefore if either x or y is a monomial of even degree [x, y] := xy − yx = 0. If both are of odd degree then [x, y] = xy − yx = 2xy has even degree and therefore commutes with z, i.e. [[x, y], z] = 0.
Properties
- Any subring or homomorphic image of a PI-ring is a PI-ring.
- A finite direct product of PI-rings is a PI-ring.
- A direct product of PI-rings, satisfying the same identity, is a PI-ring.
- It can always be assumed that the identity that the PI-ring satisfies is multilinear.
- If a ring is finitely generated by n elements as a module over its center then it satisfies every alternating multilinear polynomial of degree larger than n. In particular it satisfies sN for N > n and therefore it is a PI-ring.
- If R and S are PI-rings then their tensor product over the integers,
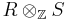 , is also a PI-ring.
, is also a PI-ring.
PI-rings as generalizations of commutative rings
Among noncommutative rings, PI-rings satisfy the Köthe conjecture. Affine PI-algebras over a field satisfy the Kurosh conjecture, the Nullstellensatz and the catenary property for prime ideals.
If R is a PI-ring and K is a subring of its center such that R is integral over K then the going up and going down properties for prime ideals of R and K are satisfied. Also the lying over property (If p is a prime ideal of K then there is a prime ideal P of R such that 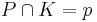 ) and the incomparability property (If P and Q are prime ideals of R and
) and the incomparability property (If P and Q are prime ideals of R and 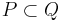 then
then 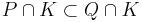 ) are satisfied.
) are satisfied.
The set of identities a PI-ring satisfies
If F := Z<X1, X2, ..., XN> is the free algebra in N variables and R is a PI-ring satisfying the polynomial P in N variables, then P is in the kernel of any homomorphism
 :F
:F  R.
R.
An ideal I of F is called T-ideal if 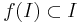 for every endomorphism f of F.
for every endomorphism f of F.
Given a PI-ring, R, the set of all polynomial identities it satisfies is an ideal but even more it is a T-ideal. Conversely, if I is a T-ideal of F then F/I is a PI-ring satisfying all identities in I. It is assumed that I contains monic polynomials when PI-rings are required to satisfy monic polynomial identities.
References
- ^ J.C. McConnell, J.C. Robson, Noncommutative Noetherian Rings, Graduate studies in Mathematics, Vol 30
- Latyshev, V.N. (2001), "PI-algebra", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=P/p072640
- Formanek, E. (2001), "Amitsur–Levitzki theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=a/a110570
- Polynomial identities in ring theory, Louis Halle Rowen, Academic Press, 1980, ISBN 9780125998505
- Polynomial identity rings, Vesselin S. Drensky, Edward Formanek, Birkhäuser, 2004, ISBN 9783764371265
- Polynomial identities and asymptotic methods, A. Giambruno, Mikhail Zaicev, AMS Bookstore, 2005, ISBN 9780821838297
- Computational aspects of polynomial identities, Alexei Kanel-Belov, Louis Halle Rowen, A K Peters Ltd., 2005, ISBN 9781568811635